You may have read Edward Belbruno’s blog on New Ways to the Moon, Origin of the Moon, and Origin of Life on Earth of October 4th. I did and was intrigued by his application of weak transfer to the origin of the Moon, so I went to his 2005 joint paper with J. Richard Gott III with the same title, published in the Astronomical Journal.
Indeed, I already knew the earlier work of Jacques Laskar on the Moon in 1993. At the time, he had proved that it was the presence of the Moon that stabilizes the inclination of the Earth’s axis. Indeed, the axis of Mars has very large oscillations, up to 60 degrees, and Venus’s axis also had large oscillations in the past. The numerical simulations show that, without the Moon, the Earth’s axis would also have very large oscillations. Hence, the Moon is responsible for the stable system of seasons that we have on Earth, which may have favored life on our planet.
The current most plausible theory for the formation of the Moon is that it comes from the impact of a Mars-size planet with the Earth, which we will call the impactor. For information, the radius of Mars is 53% of that of the Earth, its volume is 15% of that of the Earth, and its mass only 10%. Evidence supporting the impactor hypothesis comes from the geological side: the Earth and the Moon contain the same types of oxygen isotopes, which are not found elsewhere in the solar system. The Earth and Mars both have an iron core, while the Moon has none. The theory is that, at the time of the collision, the iron in the Earth and in the impactor would already have sunk into their core, and also that the collision was relatively weak, hence only expelling debris from the mantle which would later aggregate into the Moon, while the two iron cores would have merged together. Indeed, the mean density of the Moon is comparable to that of the mean density of the Earth’s crust and upper mantle.
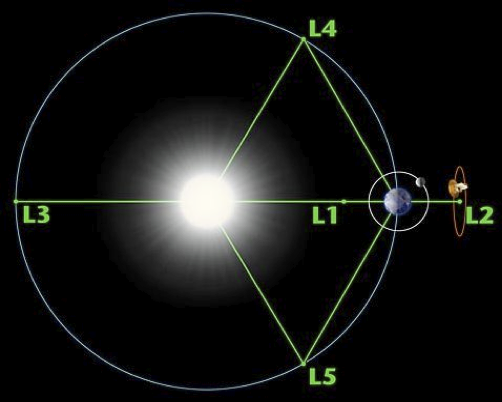
Mathematics cannot prove the origin of the Moon. It can only provide models which show that the scenario of the giant impactor makes sense, and that it makes more sense than other proposed scenarios. It is believed that the planets would have formed by accretions of small objects, called planetesimals. Because the impactor and the Earth had similar composition, they should have formed at roughly at the same distance from the Sun, namely one astronomical unit (AU). But then, why would it have taken so long before a collision occurred? Because the Earth and the impactor were at stable positions. The Sun, the Earth and the impactor form a 3-body problem. Lagrange identified some periodic motions of three bodies where they are located at the vertices of an equilateral triangle: the corresponding points for the third bodies are called Lagrange L4 and L5 points. These motions are stable when the mass of the Earth is much smaller than that of the Sun and the mass of the impactor, 10% of that of the Earth. Stability is shown rigorously using KAM theory for the ideal circular planar restricted problem and numerically for the full 3-dimensional 3-body problem, with integration over 10Myr.
Hence, it makes sense that a giant impactor could have formed at L4 or L5: this impactor is called Theia in the literature on the subject. Simulations indeed show that Theia could have grown by attracting planetesimals in its neighborhood. Let’s suppose that Theia is formed at L4. Why then didn’t it stay there? Obviously, it should have been destabilized. Simulations show that some small planetesimals located near the same Lagrange point could have slowly pushed Theia away from L4. The article of Belbruno and Gott studies the potential movements after destabilization. What is crucial is that, since the three bodies were at the vertices of an equilateral triangle, Theia and the Earth are at equal distances from the Sun. If the orbit of the Earth is nearly circular, Theia and the Earth share almost the same orbit! This is why there is a high danger of collision when Theia is destabilized.
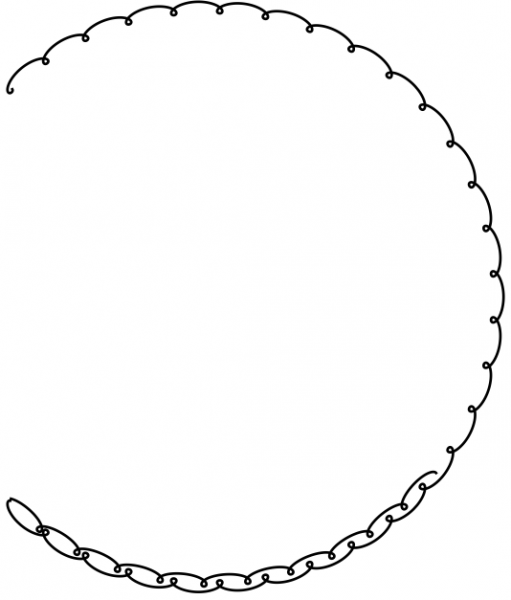
If the ejection speed were small, Theia would move back and forth along a trajectory resembling a circular arc centered at the Sun with additional smaller oscillations. In a frame centered at the Sun and rotating with the Earth (hence the Earth is almost fixed), Theia moves back and forth in a region that looks like a horseshoe (see figure).
In this movement it never passes close to the Earth. An asteroid with a diameter of 100m, 2002 AA_29, discovered in 2002, has this type of orbit. This horseshoe region almost overlaps the Earth’s orbit. For a higher ejection speed, Theia would be pushed into an orbit around the Sun with radius approximately 1 AU and gradually creep towards the Earth’s orbit: it would pass regularly close to the Earth periapsis (the point of the Earth’s orbit closest to the Sun) in nearly parabolic trajectories, i.e., trajectories borderline of being captured by the Earth. Since the speed vectors of the two planets are almost parallel, the gravitational perturbation exerted by the Earth on Theia at each fly-by is small. The simulations show that these trajectories have a high probability of collision with Earth, not so long after leaving the Lagrange points (of the order of 100 years). Note that this kind of trajectory is highly chaotic and many simulations with close initial conditions allow seeing the different potential types of trajectories.
Christiane Rousseau