We cannot see the interior of the Earth, and yet we know much about it: there is a viscous mantle below the thin solid crust. The mantle, approximately 3200km thick, surrounds the core. The core itself is divided into two parts, an outer core and an inner core. The inner core is ferrous and solid. How do we know all that? I like to tell my students that we put our “mathematical glasses”, to “see” what we cannot see with our eyes.
If the interior of the Earth is not homogeneous, then this means that the speed of signals traveling inside the Earth is not homogeneous. When large earthquakes occur, they generate strong seismic waves: these are detected and recorded by seismographs all around the world. They provide raw data that can further be analyzed. Reconstructing the interior of the Earth by analyzing what is recorded at the surface is solving an “inverse problem”. When an earthquake occurs, a first inverse problem to solve is to localize the epicenter of the earthquake.
Earthquakes generate P-waves (pressure waves) and S-waves (shear waves).
S-waves are strongly damped when traveling in viscous media, and hence not recorded far from the epicenter. This provides evidence for a liquid interior, as well as information on the thickness of the crust. On the contrary P-waves travel throughout the Earth and can be recorded very far from the epicenter.
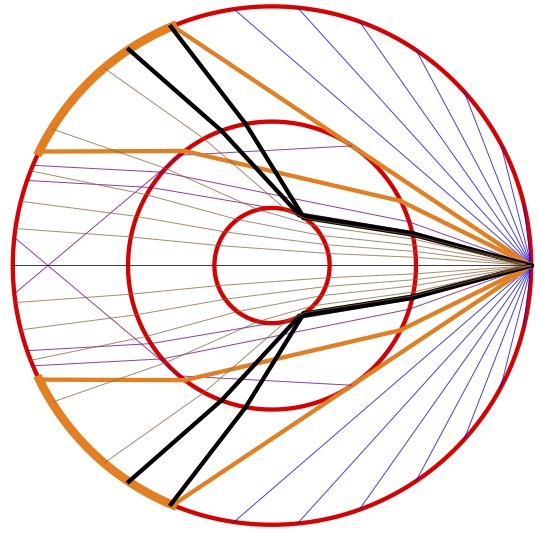
Inge Lehmann was a Danish mathematician. She worked at the Danish Geodetic Institute, and she had access to the data recorded at seismic stations around the world. She discovered the inner core of the Earth in 1936. At the time, it was known that the mantle surrounded the core. The seismic waves are traveling approximately at 10km/s in the mantle and 8km/s in the core. Hence, the waves are refracted when entering the core. This should mean the existence of an annulus region on the Earth, centered at the epicenter, where no seismic wave should be detected. But Inge Lehmann discovered that signals were recorded in the forbidden region. A piece of the puzzle was missing… She built a toy model (see figure) that could explain the observations and was later tested and adopted.
In this toy model she inserted an inner core in which the signals would travel at 8.8km/s.
If you analyze the law of refraction, namely $\frac{\sin\theta_1}{v_1}= \frac{\sin\theta_2}{v_2}$, then the equation may have no solution for $\theta_2$ if $v_1$ is smaller than $v_2$ and $\theta_1$ is sufficiently large. This means that if a wave arrives on the slow side, sufficiently tangentially to the separating surface between the two media, then it cannot enter the second medium. It is then reflected on the separating surface. Hence, seismic waves can be reflected on the inner core. This is why they could be detected in the forbidden regions.
The toy model appearing here had been completed from a figure of Inge Lehmann and illustrates the black reflected waves. Note that also some refracted waves (in brown) enter the forbidden regions.