The study of blood and the mechanism of blood clotting can be traced back to about 400 BC and the father of medicine, Hippocrates. However, the first larger advances came with the invention of a microscope and the beginning of its extensive use in research in the 17th century. Since the late 19th century until today many important breakthroughs have been made in the research of haemostatic mechanisms, leading to an excellent understanding of all of the related individual systems—the vascular system, blood cells, the coagulation pathways, and fibrinolysis. However, due to the complexity of these systems and their interaction, and difficulties of in vivo experiments, many important questions are still open for further study.
Haemostasis results in the formation of a blood clot at the injury site which stops the bleeding. The mechanism is based on a complex interaction between four different systems: the vascular system, blood cells, the coagulation pathways, and fibrinolysis. Malfunctions or changes in these systems can result in imbalance and lead to either bleeding or thrombotic disorders. Thrombosis is a life-threatening clot formation that can be caused by numerous diseases and conditions such as atherosclerosis, trauma, stroke, infarction, cancer, sepsis, surgery and many others. Thrombosis is the leading immediate cause of mortality and morbidity in modern society and a major cause for complications and occasionally death in people admitted to hospitals. Anti-coagulation medicaments that are usually administered to such patients carry a serious risk of bleeding with potentially fatal consequences. This explains the necessity of further studies of haemostasis.
During the last few decades mathematics has played an important role in the studies and analysis of blood clotting in vitro and in vivo. Each of the systems involved has been extensively modeled and analyzed using mathematical tools. This has enabled posing, evaluation and justification of biological hypothesis. First of all, the knowledge of fluid flows and hydrodynamics was used to model blood as a homogenous viscous fluid, its flow in various structures of vessels and its non-Newtonian properties. These models are usually based on Navier-Stokes equations. Furthermore, as the non-Newtonian properties of blood originate from blood cells which are suspended in blood plasma, the blood was modeled as a complex fluid in which individual cells were described. Such models allow studying of cellular interaction, the behavior and distribution of cell populations in flow. In order to describe the complex structures and behavior of individual blood cells, many cell models were developed and compared to experimentally observed characteristics and behavior, especially for erythrocytes. An example of such model is given in [1].
The complex coagulation pathways which include more than 50 proteins and their interactions were extensively modeled and analyzed by systems of partial differential equations (PDEs). The systems describe concentrations of proteins, their diffusion and reactions in vitro or in vivo (in flow). A few models were done to describe and study equally complex regulatory network of platelet interactions and the corresponding intracellular signalling.
Formation of blood clot in vivo consists of two main processes – platelet aggregation and blood coagulation. The former results in the formation of a platelet aggregate, while the latter ends by fibrin polymerization and the formation of a fibrin net. The two formations influence each other and enable the blood clot formation. The flow velocity is reduced in the platelet aggregate and protects the protein concentrations from being taken by the flow, thus enabling the coagulation reactions to occur in its core. The fibrin net which forms inside the platelet aggregate reinforces the aggregate, allowing it to grow to a necessary size and to endure the pressure from the flow.
The approaches to modeling blood clotting in flow can be divided in three main groups: continuous, discrete and hybrid models. The continuous models use mathematical analysis and systems of PDEs to describe both, the coagulation reactions [2] and the flow. In these models, blood cells (platelets) are also modeled in terms of concentrations, while the clot can be described as a part of the fluid with significantly increased viscosity. Such models correctly describe flow properties and protein concentrations in the flow. However, they are unable to capture mechanical properties and possible rupture of the clot which originate from cell-cell interactions. The second approach is to model both, the flow and individual cells, by discrete methods. There are various discrete methods that can be used to model flow, varying from purely simulation techniques to methods that are lattice discretization of hydrodynamic equations. Although suitable for description of individual cells and their interactions, such methods often do not model correctly the concentrations of proteins and their diffusion in flow.
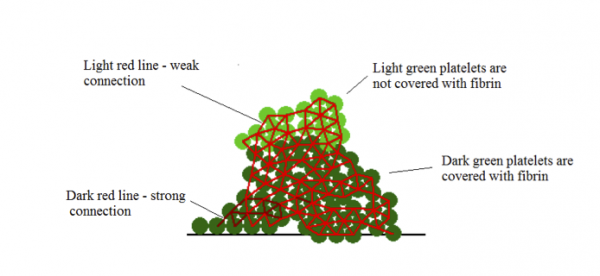
Figure 1: A scheme of a clot obtained by model described in [3]. Reprinted with permission from [3].
The third group consists of hybrid models, which combine continuous and discrete methods in an attempt to use their individual strengths and give a more suitable description of a complex phenomenon, such as blood clotting. Within hybrid models various combinations of methods are possible. An example is given in [3], where flow of blood plasma and platelets suspended in it is modeled with a discrete method called Dissipative Particle Dynamics Method (same as in [1]). The method is used to model fluid flows because it is able to correctly reproduce hydrodynamics. As platelet aggregate demonstrates elastic properties, the interactions between platelets in the model, i.e., platelet adhesion, is described by Hooke’s law. A difference is made between the weak GPIba platelet connection and the stronger connection due to platelet activation. The continuous part of the model describes fibrin concentration and diffusion in flow. The model was used to study how platelet aggregate influences and protects protein concentrations from flow. Additionally, the model has shown a possible mechanism by which platelet clot stops growing:
- In the beginning of clot growth, platelets aggregate at the injury site due to weak connections (Figure 2, a). The injury site is modelled as several platelets attached to the vessel wall. They initiate clot growth. Since the flow velocity is sufficiently high, the concentration of fibrin remains low.
- The platelet clot continues to grow due to weak connections and the flow speed inside it decreases. It makes it possible for the coagulation reaction to start, and fibrin concentration gradually increases (Figure 2, b).
- This process continues while the clot becomes sufficiently large (Figures 2, c, d). Fibrin covers a part of the clot and strong platelet connections appear inside it.
- Flow pressure exerts mechanical stresses on the clot and weak connections can rupture. In this case the clot breaks and its outer part is removed by the flow (Figure 2, e).
- Its remaining part is covered by fibrin and thus it cannot attach new platelets. The final clot form is shown in (Figure 2, f).
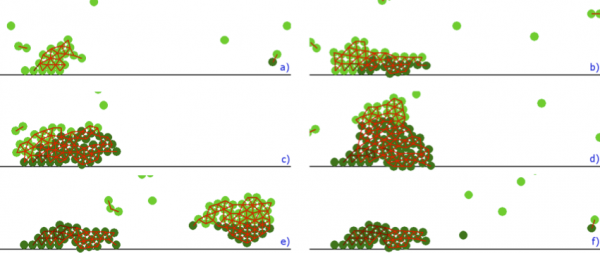
Figure 2: Platelet clot growth obtained by model described in [3]. Flow is from left to right. Reprinted with permission from [3].
The model described in [3] investigates interactions between platelet aggregate and fibrin clot. However, the overly simplified model of blood coagulation pathways results in a less correct shape of the final clot. Nevertheless, the indications of that model are confirmed by a model with a more complete description of blood coagulation pathways which also produces a more realistic final clot shape (Figure 3).

Figure 3: Final clot obtained by a more complete model of blood coagulation. Blue area denotes fibrin polymer. Flow is from left to right.
The hybrid approaches show a great potential for modelling complex phenomena. They are suitable for multiscale modelling and it can be expected that they will, in the near future, offer new insights in many biological processes of great interest.
References:
[1] N. Bessonov, E. Babushkina, S.F. Golovashchenko, A. Tosenberger, F. Ataullakhanov, M. Panteleev, A. Tokarev, V. Volpert, Numerical Simulations of Blood Flows With Non-uniform Distribution of Erythrocytes and Platelets, Russian Journal of Numerical Analysis and Mathematical Modelling, 2013, Vol. 28, no. 5, 443-458.
[2] Y.V. Krasotkina, E.I. Sinauridze, F.I. Ataullakhanov, Spatiotemporal Dynamics of Fibrin Formation and Spreading of Active Thrombin Entering Non-recalcified Plasma by Diffusion, Biochimica et Biophysica Acta, 1474 (2000), 337-345.
[3] A. Tosenberger, F. Ataullakhanov, N. Bessonov, M. Panteleev, A. Tokarev, V. Volpert, Modelling of clot growth in flow with a DPD-PDE method, Journal of Theoretical Biology 337, 2013, pp. 30-41.
Alen Tosenberger
Institut Camille Jordan
Université Claude Bernard Lyon 1, France
tosenberger@math.univ-lyon1.fr
dracula.univ-lyon1.fr