The atmosphere and ocean are central components of the climate system, where each of these components is affected by numerous significant factors through highly nonlinear relationships. It would be impossible to combine all of the important interactions into a single model. Therefore, determining the contribution of each factor, in both a quantitative and qualitative sense, is necessary for the development of a predictive model, not to mention a better understanding, of the climate system.
An approach that is appealing to mathematicians is to construct a hierarchy of models, starting from the most simple, designed to provide a “proof of concept,” and then progressively adding details and complexity, as an understanding of the factors involved in the more simple model is developed and while the necessary analysis tools are developed and refined. The question arises as to how you progress from the simple to the complex, and the challenge is to justify your choice.
One possibility is to study quantitatively accurate mathematical models of what I will call model systems, i.e., the simplification does not come through the mathematical modeling but comes simply by considering a more simple system. For example, the mathematical models of these systems do not require the use of parameterizations of sub-grid scale processes. In not so many words, these systems resemble laboratory experiments that could be, or have been, conducted.
An example of a model system is the differentially heated rotating annulus, which consists of a fluid contained in a rotating cylindrical annulus while the rotation rate and the temperature difference between the inner and outer walls of the annulus are varied (see figure). Systems of this type produce an intriguing variety of flow patterns that resemble those observed in actual geophysical flows [5]. Thus, a careful study of this system is not only inherently interesting from a nonlinear dynamics/pattern formation perspective, but can also provide insight into the dynamical properties of large-scale geophysical fluids.
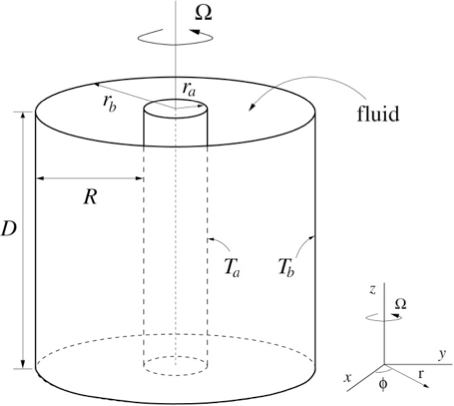
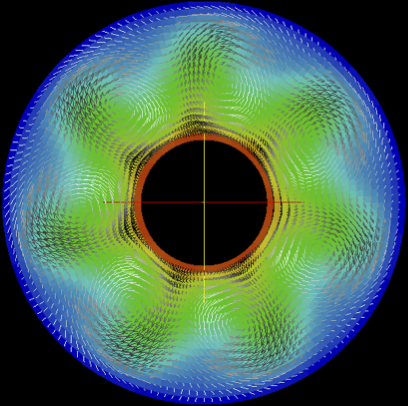
Figure 1: The differentially heated rotating annulus (left) and an example of a rotating wave (right), which is represented by a snapshot of a horizontal cross-section. The rotating wave rotates at constant phase speed, where the colours represent the fluid temperature (blue is cold, red is hot), and the arrows represent the fluid velocity.
The study of model systems is appealing for a number of reasons. First, although still very challenging, an analysis of mathematical models of these systems may be feasible if appropriate numerical methods are considered. For example, numerical bifurcation techniques for large-scale dynamical systems as discussed in [1] can be useful in the analysis of these systems. See, e.g. [4], in which bifurcation methods are applied to the differentially heated rotating annulus. Also, unlike realistic large-scale models, the results of the analysis may be quantitatively verified by comparison with observations from laboratory experiments, providing a very stringent test on the validity of any new numerical method or analysis technique that you may use.
I have emphasized the mathematical perspective, but, of course, the experiments themselves are invaluable in developing an understanding of physical phenomena of interest.
Such an approach can also be applied even when the corresponding model system cannot be replicated in the laboratory. For example, in [2] and [3], we study a model of a fluid contained in a rotating spherical shell that is subjected to radial gravity and an equator-to-pole differential heating. The results show that as the differential heating is increased, a transition from a one-cell pattern to a two- or three-cell pattern is observed, and we show that this transition is associated with a cusp bifurcation. It is also argued that this transition may be related to the expansion of the Hadley cell that has been observed in Earth’s atmosphere.
Although this approach is “standard” and has fruitfully been used for many years [5], I don’t believe that it has been fully exploited in the context of atmospheric and ocean dynamics. However, it seems that recently it has received increased interest. This is evidenced by a forthcoming book entitled Modelling Atmospheric and Oceanic Flows: Insights from laboratory experiments and numerical simulations [6], and a EUROMECH workshop of the same name that took place at the Freie Universität Berlin in September 2013 (see the workshop‘s webpage: http://euromech552.mi.fu-berlin.de/ for details). In other words, the book and workshop are focused on model systems that are studied using laboratory experiments and numerical methods with the goal of developing an understanding of atmospheric and oceanic fluid flow. The workshop was an excellent example of how bringing together open-minded people from a variety of backgrounds can lead to insight into particular issues and potentially fruitful collaborations. In particular, at the workshop, there was a very interesting mix of meteorologists, oceanographers, physicists and mathematicians. To give an idea of the variety of interesting topics that were covered, I will simply list the five plenary talks: (1) Jan-Bert Flor, from CNRS and Université de Grenoble, spoke about studying small and large scale frontal instabilities using a two-layer fluid contained in a cylindrical annulus and forced by a rotating disk at the surface; (2) Laurette Tuckerman, from the École Supérieure de Physique et de Chimie Industrielles de la Ville de Paris (ESPCI) spoke about numerical bifurcation methods for fluid dynamics problems; (3) Leo Maas, from the Royal Netherlands Institute for Sea Research (NIOZ) and the Institute for Meteorology and Oceanography Utrecht (IMAU), spoke about using both theory and experiment to study inertial waves, and their possible relationship to wave-driven flows; (4) Uwe Harlander, from Brandenburg University of Technology, spoke about using orthogonal decomposition methods to better understand the flow in the differentially heated rotating annulus , and (5) Peter Read, from the University of Oxford, spoke about using experiments to study various flow features such as heat and tracer transport, and discussed how the model systems relate to their geophysical counterparts.
For more information, I suggest the interested reader keep an eye out for the forthcoming book [6]. Many of the workshop attendees have contributed to the book, and it will certainly contain much more information about the variety of atmospheric and oceanic phenomena that are being studied using model systems.
References:
[1] H.A. Dijkstra and others. Numerical bifurcation methods and their application to fluid dynamics. Commun. Comput. Phys., 15(1):1-45, 2014.
[2] W.F. Langford and G.M. Lewis. Poleward expansion of Hadley cells. Can. Appl. Math. Quart., 17(1):105–119, 2009.
[3] G.M. Lewis and W.F. Langford. Hysteresis in a rotating differentially heated spherical shell of Boussinesq fluid. SIAM J. Appl. Dyn. Syst., 7(4):1421–1444, 2008.
[4] G.M. Lewis, N. Périnet, and L. van Veen. The primary flow transition in the baroclinic annulus: Prandtl number effects. In T. von Larcher and P.D. Williams, editors, Modelling Atmospheric and Oceanic Flows, Geophysical Monograph Series. Geopress, Amsterdam, 2014.
[5] P.L. Read. Dynamics and circulation regimes of terrestrial planets. Planet. Space Sci., 59:900–914, 2011.
[6] T. von Larcher and P.D. Williams, editors. Modelling Atmospheric and Oceanic Flows. Insights from laboratory experiments and numerical simulations. Geophysical Monograph Series. Geopress, Amsterdam, 2014.
Greg Lewis
Faculty of Science, UOIT
2000 Simcoe St. North
Oshawa, ON, Canada,L1H 7K4
Greg.Lewis@uoit.ca