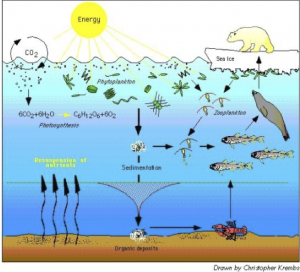
As applied mathematicians we love differential equations. So, if you are looking for an interesting set of ordinary differential equations (ODEs) with relevance for Planet Earth that is a bit more complicated than the predator-prey models, you might take a look at the so-called NPZ model of biogeochemistry. The N, P, and Z stand for nutrients, phytoplankton, and zooplankton, respectively (or, rather, for the nitrogen concentrations in these species), and the NPZ model describes the evolution of the plankton population in the ocean,
\begin{align*}
\frac{dP}{dt} &= f(I) g(N) P – h ( P ) Z – i ( P ) P , \\
\frac{dZ}{dt} &= \gamma h( P ) Z – j( Z ) Z , \\
\frac{dN}{dt} &= – f(I) g(N) P + (1 – \gamma) h( P ) Z + i( P ) P + j(Z) Z .
\end{align*}
The first equation gives the rate of change of the phytoplankton; phytoplankton increases (first term) due to nutrient uptake ($g$), which is done by photosynthesis in response to the amount of light available ($f$), and decreases due to zooplankton grazing (second term, $h$) and death and predation by organisms not included in the model (third term, $i$). The second equation gives the rate of change of the zooplankton; zooplankton increases (first term) due to grazing ($h$), but only a fraction $\gamma$ of the harvest is taken up, and decreases due to death and predation by organisms not included in the model (second term, $j$). The third equation gives the rate of change of the nutrients; nutrients are lost due to grazing by phytoplankton (first term, $f$ and $g$) and increased by the left-over fraction $1-\gamma$ of harvested zooplankton (second term, $h$) and the remains of phytoplankton (third term, $i$) and zooplankton (fourth term, $j$).
Note that the right-hand sides of the equations sum to zero, so the NPZ model conserves the total amount of nitrogen in the system,
\[
(N+P+Z) (t) = (N+P+Z) (0) , \quad t \in \mathbb{R} .
\]
The most common use of NPZ models is for theoretical investigations, to see how the model behaves if different transfer functions are used.
A survey of the merits and limitations of the NPZ model is given in the review article P. J. Franks, “NPZ models of plankton dynamics: Their construction, coupling to physics, and application,” Journal of Oceanography, 58 (2002), pp. 379–387, with an interesting follow-up article by the same author, Peter S. Franks, “Planktonic ecosystem models: perplexing parameterizations and a failure to fail,”, Journal of Plankton Research, 31 (2009), pp. 1299–1306. See also the recent textbook by H. Kaper and H. Engler, “Mathematics and Climate,” Chapter 18, OT131, SIAM, Philadelphia (2013).