A multidisciplinary group of mathematicians, biologists and hematologists from Romania is involved in developing new mathematical models of leukemia, with the goal to help the medical community better understand the disease and develop adequate treatment routines. Since for a certain patient, the evolution of the disease strongly depends on the features of his/her disease (or on specific parameters – mathematically speaking), these treatment strategies should be adapted to the patient characteristics.
Commonly, leukemia is defined as a cancer characterized by an abnormal proliferation of blood cells, caused by pathological modifications of hematopoiesis. Hematopoiesis is the process of production of all types of blood cells that includes formation, development and differentiation. At the origin of all blood cells are the hematopoietic stem cells.
When a hematopoietic stem cell enters into the cycle, it can undergo three types of division:
– Symmetric self-renewal, meaning that from a stem cell, after division, two identical stem cells will appear;
– Asymmetric division – from a stem cell will result another stem cell and a more differentiated cell (progenitors);
– Symmetric differentiation – from a stem cell will result two progenitors.
The capacity of a hematopoietic cell to proliferate is decreasing during the process of differentiation and maturation, such that a mature cell looses this ability. The cells with self-renewal ability are called stem-like cells.
There are many types of leukemias, classified according to the type and age of the cell involved in malignant transformation, so leukemias can be myeloid or lymphoid, acute or chronic. One of the most studied types of leukemia, also from a mathematically approach, is Chronic Myelogenous Leukemia (CML). The disease is believed to arise from a hematopoietic stem cell in the earliest phase of development. A chromosomal abnormality is responsible for the initiation of the disease. This abnormality is a reciprocal translocation between one chromosome 9 and one chromosome 22, the consequence being one chromosome 9 longer than normal and one chromosome 22 shorter than normal. The latter is called Philadelphia chromosome and is denoted Ph. The consequence of this process is a fusion gene causing the production of an abnormal tyrosine kinase protein, called Bcr-Abl, which is the origin of the transformation of normal hematopoietic cells to abnormal leukemic cells.
For more than 10 years, there is a standard treatment against CML, namely Imatinib mesylate, a molecular targeted drug, which is highly specific to binding with Bcr-Abl. In this way, it blocks the abnormal protein and thus removes the proliferative advantage that it provides to cancer cells. Under Imatinib, almost all patients attain hematological remission and 80% attain complete cytogenetic remission, and an estimated overall survival of 93%. at 10 years. However, Imatinib does not always completely eradicate residual leukemia cells and some patients might relapse once the treatment is stopped.
It is commonly accepted that a quantitative understanding of cancer biology needs the development of a mathematical framework to describe the fundamental principles leading to tumor initiation and expansion. Accordingly, mathematical models can be used to study cancer initiation, progression and responses to therapy. Only when the dynamics of cancer cells during therapy is understood, quantitatively precise predictions can be made about treatment success, cancer cell kinetics or therapy failure due to resistance. Thus, mathematical models are important to a complete understanding of targeted therapy.
The process of hematopoiesis, implying the cell cycle, can be described by a feedback model that uses delay differential equations (DDE) for the time evolution of the densities of cell populations involved. Such a model was first initiated by M. C. Mackey and L. Glass (see, e. g. [3]) for stem cells. When one concentrates on a single line of mature cells, leukocytes in the case of CML, two delays must be considered in the model, namely τ1 the duration of the cell cycle and τ2 the time needed for maturation.
A schematic representation of these interactions and terms involved is given below.
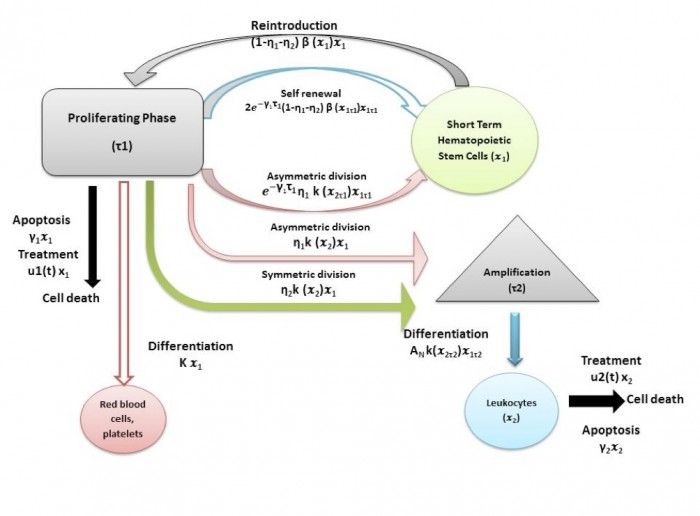
The time evolution of stem-like population is dependent on looses, through apoptosis (cell death) and through entering the cell cycle (including all kinds of proliferation: self-renew, asymmetric division and differentiation) and gains, due to the cells that entered the cell cycle τ1 time ago to self-renew or to divide asymmetrically and that leave the cell cycle and reinforce now the stem-like population. The time evolution of the mature population is dependent on looses through apoptosis and gains due to differentiation and asymmetric division. An amplification factor AN is used to describes the process of multiplication of cells through a series of divisions until they become mature cells. A linear treatment effect can be also considered when the CML cell populations are modeled.
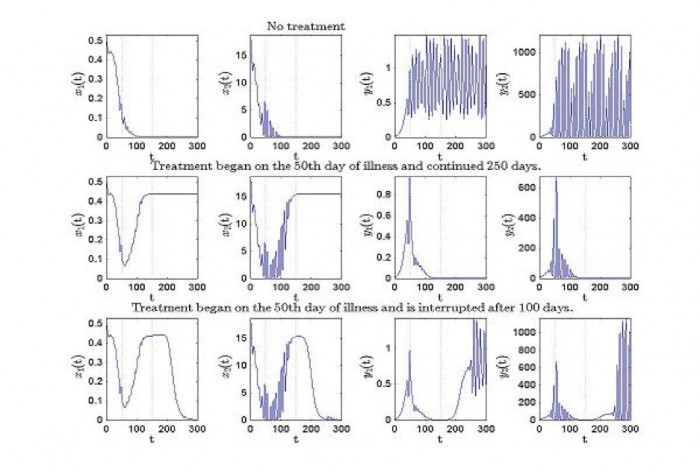
A more realistic model considers four cell densities varying in time (i.e. state variable): x1 – the stem-like healthy cell population, x2 – the healthy mature cell population, y1 – the stem-like CML population and y2 – the mature cell population. With specific parameters values for healthy and leukemia cells, the model includes competition through the feedback Hill functions that model self-renewal and differentiation and that have to depend on the total cell densities. Treatment can be also introduced, acting specifically on apoptosis, on self-renewal and on differentiation rates.
One example is in the simulations below where one can see the evolution of healthy and leukemic cells when a constant treatment is considered
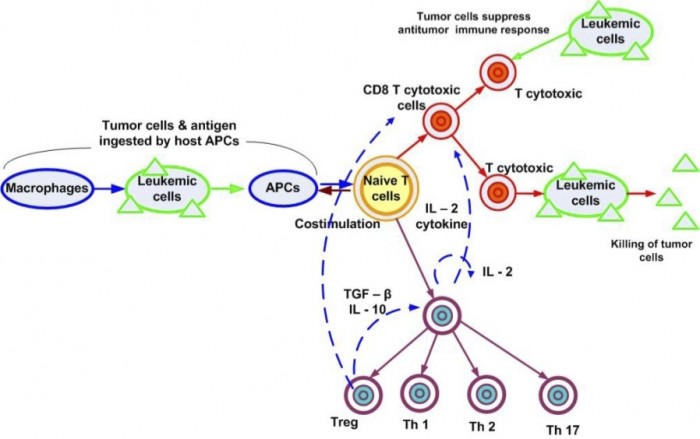
A more complex model can include in the picture the action of the immune system. The number of equations increases as well as the number of delays to be considered. Several new feedback loops regulate the interaction between the line cells of the immune system.
The study of the mathematical models starts usually by looking for equilibria and analyses their stability. Eventually a periodic evolution of the disease may be predicted due to the existence of a Hopf bifurcation when limit cycles appear. A new problem in this case is the analysis of the stability of these limit cycles (see [1]). Periodic evolutions can appear also in a context different from bifurcation of equilibria (see [2]).
Acknowledgement. The work described above has been supported by the CNCS Romania Grant ID-PNII-PCE-2011-3-0198. The team involved in these researches comprised also our colleagues S. Balea, D. Coriu, D. Candea, D. Jardan, M. Neamtu, and C. Safta.
References
[1] D. Candea, A. Halanay, I.R. Radulescu (2013), Stability analysis in a model for stem-like hematopoietic cells dynamics in leukemia under treatment, Ann. Acad. Rom. Sci., Ser. Math. Appl. 5, 1-2, 148-176.
[2] A. Halanay (2012), Periodic solutions in a mathematical model for the treatment of chronic myelogenous leukemia, Mathematical Modeling of Natural Phenomena, vol.7, no.1, 235-244.
[3] Mackey, M.C. (1997), Mathematical models of hematopoietic cell replication and control, Case Studies in Mathematical Modeling–Ecology, Physiology and Cell Biology. New Jersey: Prentice-Hall, 151–182.
Andrei Halanay and Rodica Radulescu
Department of Mathematics and Informatics
University Politehnica of Bucharest
Bucharest, ROMANIA