In a previous post, Kaitlin gave a great overview of the recent ICMS Tipping Points workshop. Today we will continue that conversation with a detailed look at efforts to understand and detect early warning signs of tipping.
Mathematical framework
Three mathematical mechanisms for tipping have been developed:
- B-tipping: there is an abrupt transition between alternative steady states that occurs due to a bifurcation.
- N-tipping: a rare noise event drives a transition between bistable states.
- R-tipping: a system parameter is varied too rapidly, causing trajectories to depart from the dynamics of the static bifurcation diagram.
A simple example of B-tipping occurs in the Stommel box model for ocean convection [2]. By increasing a freshwater forcing parameter in that model, one could force a rapid transition between thermally driven and salinity driven ocean states. Here, the transition occurs due to a saddle-node bifurcation. This turns out to be a relatively generic mechanism that is often used as the prototypical example of B-tipping: after the bifurcation point is crossed, trajectories depart the locally stable state to some alternatively stable state in such a way that the change is irreversible.
N-tipping occurs when a system exhibits bistability and there is sufficient variability in the system’s state, presumably due to noise imposed on the system, that trajectories are pushed from one equilibrium to another. The noise, perhaps a large magnitude rare event, must push the system’s state out of an equilibrium’s basin of attraction and into that of another. For this reason, the size of an equilibrium’s basin of attraction is a fundamental measure of a system’s resilience.
The last framework, R-tipping, depends on the rate at which a parameter varies with time. In a system where a single equilibrium is stable for all values of a parameter, trajectories go unstable for large excursions in phase space (due to excitability or other mechanisms) for a variation of the parameter that exceeds a critical rate. This mechanism may occur in peatland ecosystems, which are susceptible to excitability in the form of combustion.
In this report we focus on B- and N-tipping, though R-tipping is developed thoroughly by Wieczorek et al. in a paper describing the compost bomb instability [3].
Early Warning Signs
Is it possible to predict tipping in advance? Surprisingly, the answer is “yes” for many systems that can undergo B-tipping. The best known precursor results from the effect of critical slowing down on a weakly noisy signal. For systems with a deterministic component and a stochastic component (introduced perhaps as a stand-in for dynamics that happen on a fast time scale), statistical characteristics of the noise in the resulting output may change approaching a bifurcation.
Take a deterministic system with a saddle-node bifurcation as an example. A stable state of the system is characterized by the pull captured by the eigenvalues of the linearized system. These eigenvalues have negative real part. Approaching a bifurcation point by varying a parameter, one of these eigenvalues approaches zero. The pull of the system in the corresponding eigendirection diminishes, and so perturbations to the steady state close to the bifurcation point take increasingly long to return. Noise added on can be thought of roughly as repeated perturbation to the deterministic system. We expect that noise away from the bifurcation point will quickly die down to the steady state. Close to the bifurcation though, noise can push the system away from its steady state. If the noise is regular, and satisfies some modest criteria [4], then one would expect the noise (relative to the deterministic signal) to become more correlated and more volatile approaching the saddle node bifurcation. Thus, given certain criteria, one would expect to see signals in the autocorrelation function of the noise and in the variance of the noise as a system approaches a bifurcation point.
Intrinsic noise occurs in many natural systems, and given that the underlying dynamics of a system roughly satisfy the criteria of critical slowing-down methods, one may search for increased autocorrelation and variance in noise from real data. One source of data that may be conducive to this kind of analysis is the paleoclimate proxy record. These proxies are correspondences between strongly correlated variables within the climate, like correspondences between oxygen isotope ratios (which can be observed in ice-core records) and past temperature. If one were to assume that there was some strongly deterministic signal in the proxies recording Dansgaard-Oeschger events, then the noise about this signal could be analyzed for increased correlation and variance. Dakos et al. do this for a number of proxy records, and find increased autocorrelation signals approaching what appear to be abrupt transitions [5].
This sort of analysis may provide a test of critical slowing-down methods, as abrupt transitions can be readily observed in these records. However, it is unclear whether these transitions constitute what we characterize as tipping. It is possible that dynamics were such that a small change of parameters had a large impact on the system state, but in a reversible way. In this case, no bifurcation occurs. Rather, there is a single steady state that is stable throughout the transition.
Since the rate of change of the steady state with respect to the parameter is steep, one may also expect to see some of the same hallmarks of critical slowing down that one would see with a bifurcation. Though in either hypothesis the state of the system is strongly affected, the existence of a bifurcation may imply bistability and hysteresis, and therefore some degree irreversibility. By comparison, an abrupt transition that is brought on by a steep response curve should be reversible.
Another caveat is that in many cases, the size of a steady state’s basin of attraction decreases approaching the bifurcation point. When there is bistability, noise can more easily push the trajectory of a system out of the basin of one steady state and into another. A transition that happens this way is considered N-tipping. N-tipping transitions depend on a rare event in the noise process causing the system to transition between bistable states. For this reason, prediction in this case is difficult. N-tipping near a bifurcation point presents an important limitation in the use of critical slowing down as an early warning sign. Critical slowing down cannot necessarily give information about when a transition will occur, but simply that it can occur. This, though perhaps unsatisfying, is still useful. If one can identify aspects of the climate that bear the hallmarks of critical slowing down, then measures can be taken to reverse the direction of change to avoid catastrophic transition.
While these signals are generic in the sense that they may appear wherever the generic saddle-node bifurcation mechanism occurs, many have cautioned against using these indicators without some understanding of the underlying dynamics. In particular, one must avoid the prosecutor’s fallacy, which in probabilistic terms means that $P(A|B)$ ≠ $P(B|A)$ unless $P(A)$ = $P(B)$. In the context of early warning signs, we can think of $A$ as “the occurrence of B-tipping” and $B$ as “the appearance of early warning signs”. Simply put, observing a warning sign does not imply that B-tipping is occurring! It is important to formulate a mathematical model because a model can be analyzed, criticized, and modified. This is key to a sound hypothesis about what is observed in data. If the model is consistent with a bifurcation-induced transition, then this lends credence to the hypothesis that increased correlation and variance herald tipping.
Early warning signs derived from critical slowing down offer promise as broadly applicable tests for a natural system’s resilience to change and proximity to abrupt transition. They are certainly not foolproof: in addition to the pitfalls listed above, one must be careful to verify that the noise satisfies certain statistical properties and that the results are significant (which requires a sufficiently large number of observations). It has been shown that lag-1 autocorrelation used in conjunction with variance minimize Type I and II error in controlled settings [7]. With some additional modeling, it may be possible to develop even more precise indicators for a specific system.
References:
-
[1] “Tipping points: fundamentals and applications.” International Centre for Mathematical Sciences, n.d. Web. 16 Sept. 2013.
[2] Stommel, H. (1961). Thermohaline convection with two stable regimes of flow. Tellus, 13(2), 224–230.
[3] Wieczorek S, et al. (2011) Excitability in ramped systems: The compost-bomb instability, Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences, vol. 467, no. 2129, pages 1243-1269.
[4] Scheffer, M. et al. (2009) Early-warning signals for critical transitions. Nature 461, 53-59.
[5] Dakos, V., et al. (2008) Slowing down as an early warning signal for abrupt climate change. Proceedings of the National Academy of Sciences of the USA, 105(38), 14308-14312.
[6] Ditlevsen, P. D., & Johnsen, S. J. (2010). Tipping points: Early warning and wishful thinking. Geophysical Research Letters, 37(19). doi:10.1029/2010GL044486
[7] Beaulieu, C. Early warning signals for critical transitions: sense, sensitivity and specificity. Invited talk. ICMS Tipping Points: fundamentals and applications. 12 Sept. 2013.
Karna Gowda
Northwestern University
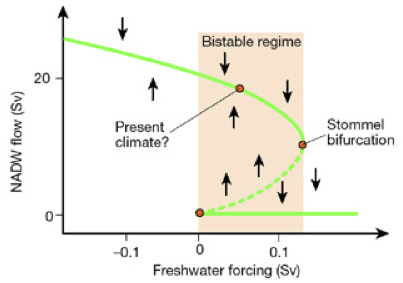
![Figure from [4]](http://mpe.dimacs.rutgers.edu/wp-content/uploads/2013/09/Figure-from-4.png)
![Figure from [6]](http://mpe.dimacs.rutgers.edu/wp-content/uploads/2013/09/Figure-from-6.png)
Pingback: Early Warning Signs of Tipping | Karna Gowda