Fausto Gozzi
Libera Università Internazionale degli Studi Sociali (LUISS)
Rome
1. Some history
The theory of optimal control, starting in the 50’s, has found many applications in various areas of natural and social sciences. Over the years, as more difficult applied problems have been attacked, the theory has made advances. Here we consider the optimal control theory of infinite dimensional systems that has recently found interesting applications in theoretical economics so that economic models can be made more realistic.
These infinite dimensional systems are usually dynamical systems whose evolution is described by a partial differential equation (PDE) or a delay differential equation (DDE). They are infinite dimensional in the sense that they can be rephrased as standard ordinary differential equations (ODE’s) in abstract infinite dimensional spaces such as Hilbert or Banach spaces.
The study of optimal control problems of such systems began in the 70’s with the two main methods of optimal control theory: Bellman’s Dynamic Programming and the Pontryagin Maximum Principle. The main examples motivating such theory usually came from physics and engineering applications, but starting in the 90’s more and more work in the field was motivated by economic and financial applications.
Here we discuss the use of the Dynamic Programming Method with the associated Hamilton-Jacobi-Bellman (HJB) equations for a particular family of such problems that has been recently studied, namely, the optimal control of heterogeneous systems.
2. Why model heteorogeneity in economics?
Economic models have traditionally been built under several simplifying assumptions for a number of reasons, including tractability. Among the reasons, we consider the following three: the representative agent, the homogeneity of capital, and the absence of a spatial dimension.
Considering a single agent to represent the average behaviour of a large number of consumers, for example, greatly simplifies the analysis of an economic system and has enabled the development of a large and coherent body of economic research. As an example, neoclassical growth theory, which has been tremendously influential, considers a representative consumer and a representative firm in place of thousands (or millions) of separate consumers and firms.
Capital homogeneity, which is the lumping together all the forms of capital investment, including human capital and physical capital, is a second simplifying assumption often made in economics. Again the neoclassical growth theory makes this assumption and treats capital investments at different times (vintages) as identical. This, of course, is hardly realistic, since new vintages typically embody the latest technical improvements and are likely to be significantly more productive. This was clearly stated by Solow in 1960 when he wrote “…This conflicts with the casual observation that many if not most innovations need to be embodied in new kinds of durable equipment before they can be made effective…”
Finally, while space has been recognized as a key dimension in several economic decision-making problems for quite a long time, it has been seldom explicitly incorporated even in the models of growth, trade and development where this dimension seems natural. This trend has lasted until the early 90’s as mentioned by Krugman (2010) in a retrospective essay: “…What you have to understand is that in the late 1980s mainstream economists were almost literally oblivious to the fact that economies aren’t dimensionless points in space and to what the spatial dimension of the economy had to say about the nature of economic forces…”
Beyond analytical simplicity and internal consistency, the prevalence of such simplifying assumptions is due to the widely shared belief that departing from these assumptions would NOT improve our understanding of the main mechanisms behind the observed economic facts and would, at the same time, make economic models analytically intractable. But since the late 90’s, accounting for heterogeneity has become an essential aspect of research. The representative agent assumptions and other homogeneity assumptions have been heavily questioned, and new analytical frameworks explicitly incorporating heterogeneous agents and/or goods have been put forward and studied. Basically, this evolution is due to two important factors.
- a. A major factor is the emerging view that heterogeneity is needed to explain key economic facts. For example, the resurgence of the vintage capital work in the late 90’s is fundamentally due to new statistical evidence on the price of durable goods in the US, showing a negative trend in the evolution of the relative price of equipment, only compatible with embodied technical progress, thus making legitimate the explicit vintage modelling of capital.
- b. At the same time, the rapid development of computational economics—especially in the last decade—makes it feasible to deal with models having heterogeneous agents. Special issues of the reference journal in the field, Journal of Economic Dynamics and Control, have been devoted to this specific area (issue 1 in 2010 and issue 2 in 2011), suggesting that it is one of the hottest areas in the field of computational economics.
3. An example of results
We consider, for example, the vintage capital model. Beginning with the easiest neoclassical growth model (the so-called AK model) one generalizes it to the case when capital is heterogeneous in the sense that capital is differentiated by its age (vintage capital). The basic equation (the State Equation in the language of optimal control) becomes a differential delay equation. Using Bellman’s Dynamic Programming method it becomes possible to characterize the optimal trajectories, which “should” describe the behavior of economic system.
In this case the introduction of heterogeneity allows a more faithful description of the features of this economic system. Indeed, in the graph below (Boucekkine et al.) one can see the behavior of the output y(t) (the production) of the model (after a detrending which is done for the sake of clarity) in the two cases:
− the horizontal line is the output in the classical AK model;
− the oscillating line is the output in the AK model with vintage capital.
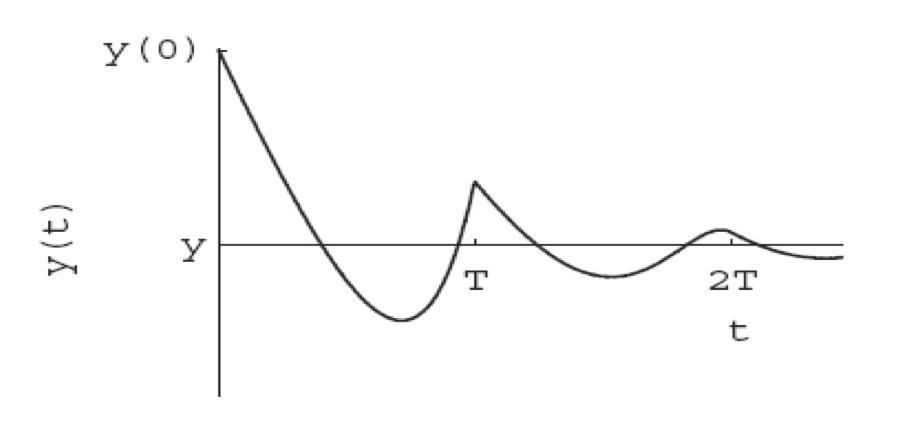
Fluctuations of the output is a well known feature that is captured with infinite dimensional optimal control models.
4. Further directions
Further work needs to be done with heterogeneity resulting from the spatial and population distribution of economic activity. This heterogeneity is a key feature of contemporary economic systems and a deep study of such models incorporating heterogeneity should both provide more insight into the behavior of such systems and more help for policy makers making decisions. In particular the issues under study are:
− environmentally sustainable growth regimes;
− land use;
− the socio-economic and public finance problems related to ageing on one hand, and to epidemiological threads on the other;
− to incorporate the age-structure of human populations in the analysis of key economic decisions like investment in health and/or investment in pension funds both from and the private and social optimality points of view.
References
Giorgio Fabbri and Fausto Gozzi. Solving optimal growth models with vintage capital: the dynamic programming approach. Journal of Economic Theory 143 (2008), no. 1, 331–373.
R. Boucekkine, O. Licandro, L.A. Puch, F. del Rio. Vintage capital and the dynamics of the AK model. Journal of Economic Theory 120 (2005), no. 1, 39–72.