This contribution can be seen as a follow-up of that of July 5 where I discussed the Earth as a deformed sphere that geodesists choose to approximate by the geoid: the geoid is the level surface of the gravitational field corresponding to the mean sea level (MSL).
It has been known since Gauss that it is not possible to draw maps of the Earth that preserve ratios of distances. But it is possible to find projections of the sphere that preserve ratios of areas: these projections are called equivalent. A typical example is the horizontal projection of Lambert, which was in fact already known from Archimedes. It is also possible to find projections of the sphere that preserve angles: these projections are called conformal. One of them is the stereographic projection, which was already known to the Greek Hipparchus. A second one is the Mercator projection. It is remarkable that Mercator and Hipparchus could prove that their respective projections are conformal without the use of differential calculus.
But if we consider the geoid, is it possible to draw conformal maps of it? The answer is still positive, but the proof is more subtle. For instance, in the case of conformal mapping, we find elements of a proof in the book “Differential Geometry of Curves and Surfaces” of Do Carmo, but he refers to “Riemann surfaces” by Lipman Bers for a full proof. The proof comes to show that a regular differentiable surface can be given a conformal structure, i.e., is a Riemann surface, and the conformal structure is obtained through solving a Beltrami equation.
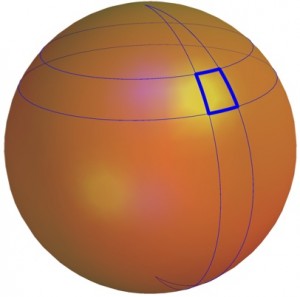
Let us discuss the particular case where the geoid is rotationally symmetric around the Earth’s axis, by generalizing Mercator’s strategy. We consider two angles: $L$ is the longitude and $\ell$ the latitude, and we can make the hypothesis that any half-line from the center of the Earth along the direction corresponding to longitude $L$ and latitude $\ell$ cuts the Earth in a point at a distance $R(\ell)$ from the center of the Earth. The intersection curves of the geoid with the half planes where $L$ is constant are called the meridians of the geoid, and we wish them to be represented by vertical lines on the map. Similarly, the intersection curves of the geoid with the cones where $\ell$ is constant are called the parallels of the geoid, and we represent them on the map by horizontal segments of length $2\pi$, parameterized by $L$. Let us consider a small region corresponding to a width of $dL$ and a height of $d\ell$ and with corner at $(L,\ell)$ on the geoid. On the geoid, the length of this small region in the direction of the meridians is approximately $\sqrt{R^2+ (R’)^2}d\ell$ and its width (in the direction of the parallels) is approximately $R\cos \ell \;dL$. Hence, the diagonal makes an angle $\theta$ wit the parallels such that $\tan \theta \simeq \frac{\sqrt{R^2+ (R’)^2}}{R\cos\ell} \frac{d\ell}{dL}$.
Now we must compute the projection on the map of a point of longitude $L$ and latitude $\ell$. Its coordinates will be $(L, F(\ell))$. On the map, the small region is represented by a rectangle of width $dL$ and of height $F'(\ell)d\ell$. Hence, the diagonal makes an angle $\theta’$ with the horizontal direction, such that $\tan\theta’= F'(\ell)\frac{d\ell}{dL}$.
The mapping is conformal if $\theta’= \theta$, which means that $F'(\ell)= \frac{\sqrt{R^2+ (R’)^2}}{R\cos\ell}$, from which $F$ can be obtained by integration.
Note that we could have used the same technique to find an equivalent mapping. If we let $r(\ell)= \frac{R(\ell)}{R(0)}$, then the projection preserves ratios of areas if $F'(\ell)= r\cos\ell\sqrt{r^2+ (r’)^2}$, from which $F$ can again be obtained by integration.
Christiane Rousseau