If we model the Earth as a sphere of radius $R$, then the altitude of a point is its distance to the center of the Earth minus $R$. But we know that the surface of the Earth is not exactly a sphere and is, in fact, better approximated by an ellipsoid. Again, it is possible to generalize the definition of altitude for an ellipsoid of revolution. For a given point $A$, we consider the segment joining it to the center $O$ of the ellipsoid. The half-line $OA$ cuts the ellipsoid in a point $B$, and the altitude is the difference between the length of $OA$ and that of $OB$.
So far, no problem. However, the Earth is not a perfect ellipsoid of revolution. Then what is the center of the Earth, and what means altitude? When we represent the Earth by a solid sphere or ellipsoid, we implicitly assume that we have a surface that approximately fits the surface of the Earth’s oceans. (Of course, the surface of the oceans varies with the tides, and we must consider the mean surface of the Earth’s oceans.) This surface is called a geoid. We then add the topographical details to the geoid.
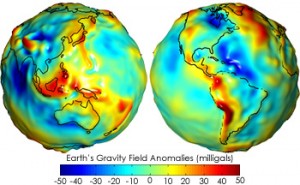
The point of view taken in geodesy is to consider the gravitational field generated by the Earth. On the surface of the Earth, the gravitational field is directed toward the Earth’s interior, and the center of gravity of the Earth, which is a natural candidate for the Earth’s center, is a singular point of this gravitational field. The gravitational field comes from a potential, and it is natural to consider the level surfaces of this potential. Thus, a geoid will be an equipotential of the gravitational field, chosen to give the best fit of the surface of the oceans with the geoid corresponding to the mean sea level. The differences between the geoid and an ellipsoid come not only from the presence of mountains, but also from the density variations inside the Earth. The geoid is then taken as the surface of altitude zero, and the altitude of a point $A$ is defined as its distance to the geoid measured along the normal through $A$ to the geoid. This normal is easily determined in practice, since it corresponds to the vertical as indicated by a carpenter’s level or a surveyor’s plumb bob. Let $O$ be the center of the geoid and $B$ the intersection point of the half-line $OA$ with the geoid. In general, the altitude of $A$ is not exactly equal to the difference between the length of $OA$ and that of $OB$, because the normal to the geoid through $A$ may not pass through $O$.
The difference between the geoid and an ellipsoid of revolution approximating the Earth can be up to 100 meters; hence, it is quite significant. The first GPS would calculate the altitude as the distance to an ellipsoidal model of the Earth. Modern receivers are now able to correct this measurement and give the real altitude over the geoid.