How fast does water flow through sand or soil? Maybe not so fast, but everyone has seen water soak into beach sand and garden soils. Most people have also noticed a concrete sidewalk soaking up a little water as rain begins to come down. But how fast does water flow through a rock? The obvious answer is incorrect: water does indeed flow through rocks. Not the rock grains themselves, but it can squeeze through the pore spaces between the rock grains. We say that the Earth’s subsurface is porous, and that it is a porous medium.
Fluid flow through the planet’s subsurface is critically important to many ecological and economic activities. Subsurface flow is an important part of the entire water cycle. In fact, the United States Geologic Survey estimates that, worldwide, there is 30 times more groundwater stored in aquifers than is found in all the fresh-water lakes and rivers. Unfortunately, contaminants sometimes leach out of storage sites, either from above ground tanks or through underground containment barriers, and travel through the Earth. Petroleum and natural gas are extracted from the subsurface by inducing these fluids to flow to production wells. To mitigate the effects of greenhouse gas accumulation in the atmosphere, technologies are being developed to sequester carbon dioxide, extracted from power plant emissions, in deep underground reservoirs. These and many other situations make it important that we have the ability to simulate the flow of fluids in the subsurface. The simulations give us a visual and quantitative prediction of the movement of the fluids, so that scientists, engineers, and regulators can design appropriate steps to, e.g., protect the natural ecosystem and human health, optimize the economic benefit of the world’s underground natural fluid resources, and minimize unintended impact on the natural environment.
So, how fast does fluid flow in porous media? In 1856, a French Civil engineer by the name of Henri Darcy determined through experimental means the speed at which fluid flows through a sand column when subjected to pressure. He gave us his now famous Darcy’s Law, which states that the fluid velocity is proportional to the pressure gradient. Subsequent experiments verified that the law holds for all types of porous media. The proportionality constant in Darcy’s law, times the fluid viscosity, is called the permeability of the porous medium. The permeability is a measure of how easily fluid flows through a rock or soil.
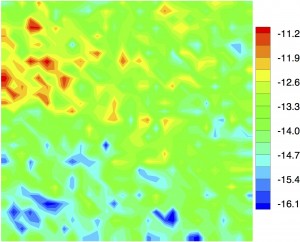
There are many difficulties associated with simulating the flow of fluid through a natural porous medium like a groundwater aquifer or a petroleum reservoir. One of them is dealing with the extreme heterogeneity of a natural rock formation. One sees this extreme heterogeneity in outcrops, which are rock formations that are visible on the surface of the Earth, such as is often seen from a roadway which has been cut into a hill or mountain. In Figure 1, we show results from researchers at the University of Texas at Austin’s Bureau of Economic Geology, who measured the permeability of an outcrop. The permeability is shown on a log scale, and it varies from $10^{-16}$ (blue) to $10^{-11}$ (red) over a few meters. That is, the fluids can be moving about 100,000 times faster in one area of the rock than another less than a meter away.
An underground aquifer or reservoir domain can be very large, spanning a few to hundreds of kilometers. Normally a simulation of fluid flow will involve a computational grid of cells that cover the domain. The fastest supercomputers can possibly handle enough cells so that each is about ten meters square. But at that scale, we have lost all details of the permeability’s heterogeneity, and consequently many important details of the fluid flow! So the challenge is to find a way to resolve the details of the fluid flow without using a computational grid that is able to resolve the flow. It sounds like a contradiction.
This is one place where mathematics and mathematicians can help. Since we cannot resolve all the details of the flow, let us make as our goal the ability to approximate the average flow within each grid cell, by simplifying the geologic structure of the porous medium. That is, we desire to replace the complex heterogeneous porous medium within a grid cell by a simple homogeneous porous medium with an average value of permeability, as depicted in Figure 2. But what should this average permeability be? It should be chosen so that the average amount of fluid flowing through the grid cell is the same for the true and fictitious media.

Figure 2. The heterogeneous porous medium is replaced by a homogeneous one with an average permeability k, chosen so that the average amount of fluid flow is the same.
It is fairly easy to solve the differential equations governing the flow of fluid in simple geometries. For a layered porous medium, there are two possibilities. As depicted in Figure 3, when the flow is going along with the geologic layers, the correct way to average the permeability is to take the usual arithmetic average. In this case, (k1 + k2)/2.
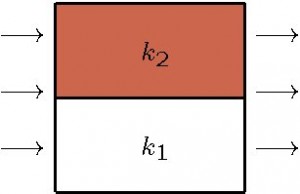
Figure 3. Flow going along with the geologic layers requires arithmetic averaging of the permeability k.
When fluid flows so that it cuts through the layers, as depicted in Figure 4, the arithmetic average permeability does not give the correct average fluid flow. This is perhaps easy to see by considering the possibility that one of the layers becomes impermeable, say k1=0, so that fluid cannot flow through it. In this case, there will be no flow through the entire grid cell. But the arithmetic average is k2/2>0, and we should expect some fluid flow through the grid cell. The correct average to take is the harmonic average, which is the reciprocal of the arithmetic average of the reciprocals, i.e., 2/(1/k1 + 1/k2).
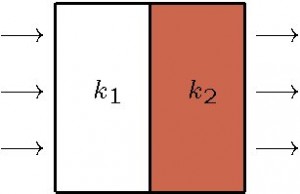
Figure 4. Flow that cuts through the geologic layers requires harmonic averaging of the permeability k.
The harmonic average is always less than or equal to the arithmetic average. But what about a genuinely heterogeneous porous medium like that shown in Figure 5? More sophisticated averaging techniques must be used, such as arise in the mathematical theory of homogenization. It can be proven that the correct average always lies between the harmonic and arithmetic averages, so our layered case actually gives the extreme cases of the problem. In fact, homogenization is also able to account for the fact that porous media may be anisotropic, i.e., they do not behave the same in every direction. The example in Figure 5 is anisotropic, since perhaps one can see that as fluid tries to flow from left to right, it will also tend to flow upwards a bit as well.
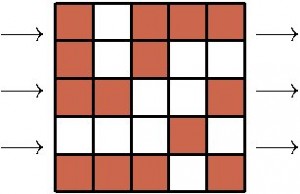
Figure 5. Flow through a heterogeneous geologic region requires more complex averaging of the permeability.
These averaging techniques work well for even very complex geology. For example, consider the heterogeneous rock shown in Figure 6, which is a complex mixture of fossil remains, limestone, sediments, and vugs, which are large open spaces in the rock. Without a theoretically sound mathematical averaging technique, would you like to guess the average permeability of this rock?
More complex numerical models have also been developed by mathematicians, that not only give the correct average flow, but also attempt to recover some of the small scale variability of the flow. Such multi-scale numerical methods are an active area of research today. These methods can allow scientists and engineers to simulate the flow of fluids in the subsurface in an accurate way, even on computational grids too coarse to resolve all the details. It almost seems like magic. But it is not magic, it is mathematics.
Todd Arbogast
Professor of Mathematics
University of Texas at Austin