For the past nine weeks, I had the privilege to teach a Massive Open Online Course (MOOC) on image and video processing. The first half of the class was dedicated to topics that everybody should know in the subject, like JPEG, JPEG-LS, the Hough Transform, histogram equalization, Otsu’s algorithm (like I always say to my students, if you didn’t learn that at school in your image processing class, you should ask for your money back!), and the second half was dedicated to advanced topics like partial differential equations and sparse modeling.
The experience of teaching a MOOC, while extremely time consuming, is incredibly rewarding, and this has been the subject of many articles in the popular press already and is the topic of multiple in campus forums. What I want to express here instead is that such experience gave me the chance once again to realize and to teach how important mathematics is in image and video processing. Basically, all fundamental algorithms have an extraordinary mathematical support. JPEG for example, which is without any doubt the most successful image processing algorithm, is based on critical tools from Fourier analysis and information theory. Its most recent continuations, JPEG-2000 and JPEG-LS (both closely connected to the algorithms roaming Mars in both the previous and the current expeditions) are based again on fundamental mathematical concepts like wavelets, Golomb coding, and context modeling.
The use of partial differential equations and differential geometry brought not only some top mathematicians to work in image processing, but numerous state-of-the-art results as well. More recently, compressed sensing and sparse modeling provided yet another example of how important mathematics is in this area. A propos this, in collaboration with the National Geospatial-Intelligence Agency, we have recently demonstrated the use of sparse modeling and dictionary learning for hyperspectral image classification, including from severely undersampled data. These types of techniques are critical to learn the state of our planet.
Mathematics will continue to play a critical role in image and video processing; it has done it already for planet Earth and beyond.
A collage of image processing, logo of the MOOC class.
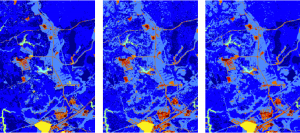
Original ApHill hyperspectral image, followed by mapping (classification) after reconstruction from only 2% of the data, without including spatial coherence in the process, and the same with spatial coherence.
Guillermo Sapiro
Edmund T. Pratt, Jr. Professor
Dept of Electrical and Computer Engineering
Duke University