“Mathematicians listen as the Earth rumbles… ” This was the title of the fourth MPE Simons Lecture given by Ingrid Daubechies in Montreal, Canada, on April 10. Her splendid lecture was delivered in French, but both English and French videos of the lecture will be on display soon on the Simons website.
Too often, we limit Mathematics of Planet Earth to climate change and sustainability problems. On the contrary, this lecture was totally fitting under the first theme of MPE, namely a “planet to discover”. The lecture of Ingrid Daubechies was related to her personal work with geophysicists and very recent results on the problem of understanding the formation of the volcanic islands.
The rocks in the bottom floor of the oceans are much younger than those of the continents. On the bottom of the oceans, the most recent rocks are along the ridges where tectonic plates diverge. And indeed, there is volcanic activity along these ridges, with new rocks being formed by magma coming up from the mantle to the surface. But there are also isolated volcanic islands, like Hawaii, Tahiti, the Azores, Cap Verde, etc. If we look to the archipelago of Hawaii, all islands are aligned, and their age increases from the largest island at one end to the smaller islands further down. This has suggested to the geophysicists that the islands were formed because of a plume, i.e., a kind of volcanic chimney through the mantle. Recall that the mantle goes as deep as half the radius of the Earth. Since the surface plate is moving, this could explain the successive formation of the aligned islands, the difference of age of which would be calculated from the distance between the islands and the speed of the tectonic plates.
But additional evidence is needed for the conjecture to be accepted by the scientific community. For instance, one would like to “see” the plume. One tool for exploring the interior structure of the Earth is remote sensing: one sends waves (signals) and analyzes the signals reflected by the boundary of some layer or refracted inside different layers. But plumes are located so deep under the Earth’s crust that the usual signals are not powerful enough to be of any help. The only waves that carry sufficient energy to analyze details at such a depth are the seismic waves generated by large earthquakes.
Large databases exist which contain the recordings of these seismic waves by seismic stations around the world. So the data exist. We then need an appropriate tool to analyze them. The problem is not trivial. The plumes are very thin regions and, moreover, the difference of the speed of a seismic wave through a plume is only of the order of 1%.
In 2005, seismologists Tony Dahlen and Guust Noleta approached Ingrid Daubechies to see if wavelets could help in their venture. Indeed, the promising results of the student Raffaela Montelli (pictured) had shown that seismic methods could be used to capture regions of perturbations of the pressure waves (P-waves) of earthquakes, see figure.
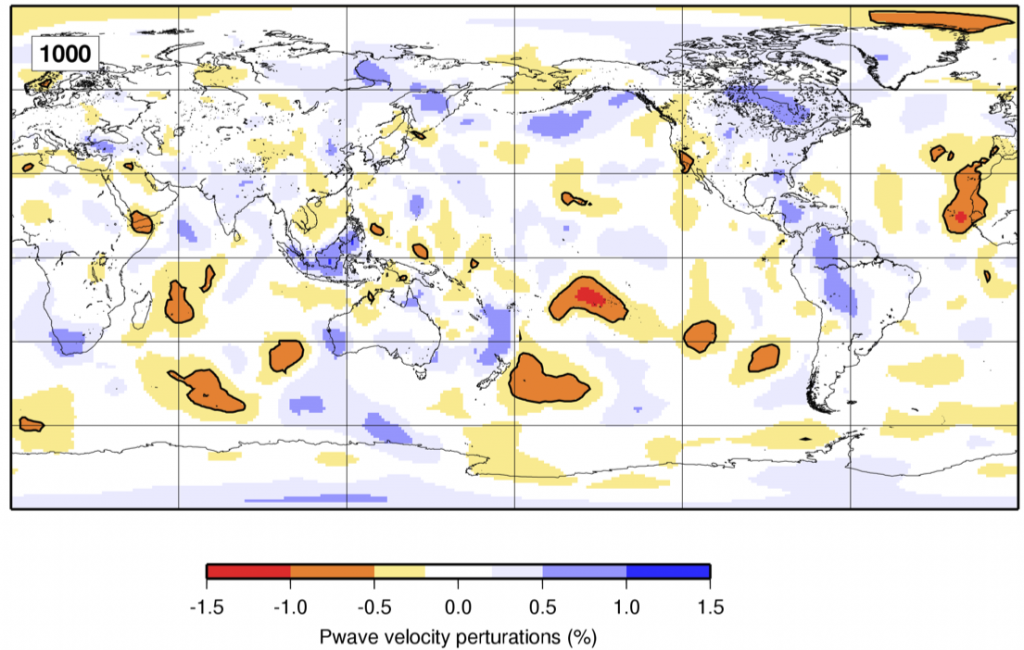

Such regions overlapped exactly the regions with isolated volcanic islands: the temperature of the ocean floor was higher in these regions. But, as mentioned above, the plumes are very thin and the difference of speed of seismic P-waves very small in these regions. Hence, there is a large risk of errors in the numerical reconstruction of the inner structure of the Earth, unless we use an appropriate tool. This is where wavelets proved useful. They are the perfect tool to analyze small localized details. Moreover, one can concentrate all the energy in small regions and neglect the other regions.
In her lecture, Ingrid Daubechies gave a short course on wavelets adapted to digital images made of pixels. A gray-tone image is just an array of numbers giving the gray tone of each pixel. From this matrix, one constructs four smaller matrices consisting of either horizontal or vertical averages of neighboring pixels taken 2 by 2, or horizontal or vertical differences of neighboring pixels taken 2 by 2. One can iterate the process on the matrix of horizontal and vertical averages. She explained how wavelets allow compressing information and how we can extract very fine details in a local region while keeping the size of the data manageable. The use of wavelets to construct the images allows removing all errors in numerical reconstructions and making sure that the special zones identified in the image are indeed special. She showed clean images produced with wavelets in which artificial special regions had been removed, and she could announce “hot off the press” that she and her collaborators had obtained the first results with the whole Earth, and real data!
Christiane Rousseau