I was asked to write this blog because I am a participant in the upcoming MPE workshop, Batteries and Fuel Cells, running November 4-8 in Los Angeles. This is part of a term-long thematic program, Materials for a Sustainable Energy Future, organized by the Institute for Pure and Applied Mathematics (IPAM) at UCLA. I was invited because I was involved with a decade-long project (1998-2008) modeling hydrogen fuel cells. This was a very applied project in collaboration with scientists at Ballard Power Systems, a Vancouver company that is a world leader in the development of these devices. It was a group project, with several other faculty members participating, notably Keith Promislow who became a close personal friend. In this blog I’ll give a description of what we did on that project. The activity then serves as an example of how academic mathematicians can become involved in work that has a direct impact on the world.
Hydrogen fuel cells are of interest as an alternative energy technology. They are electrochemical systems that combine hydrogen and oxygen (from air) to produce electrical energy. They have potential for use in many applications, including automotive, stationary power and small-scale power for mobile electronics. Unlike batteries, the energy source (hydrogen gas) flows through the device and so they are not intrinsically limited in capacity. These devices fit into a possible new energy economy in which energy coming from a number of sources including renewable ones is stored as hydrogen gas. Fuel cells have two main benefits over existing technology. They are very efficient when fueled by hydrogen, and the only end product is water, so they are non-polluting in use. It should be said that currently, hydrogen is mainly produced by refining fossil fuels. These devices are now proven technology. However, they are more costly than current technologies. The development of new materials that fuel cell cost and increase their lifetime of use is the current research focus in the industry. Models of the kind of materials used in this industry is the subject of my current research, with Keith.
The project I was involved with began under the umbrella of MITACS, a Canadian network that supported industrial mathematics activity from 1999 to a few years ago. Actually, MITACS still exists but has broadened its scope to cover all disciplines (so the “M” no longer stands for Mathematics). There were a number of connections that led to the collaboration, but the one that makes the most interesting story starts with John Kenna, who was an engineer at Ballard at that time. He had been trained as a fuel cell engineer, but had worked at Hughes as an aeronautical engineer before coming to Ballard. Most of the design work for aircraft now is done with computational tools. That is, new design ideas are not made as physical models and tested experimentally. Rather, the physics of airflow and the behavior of the aircraft structure in response to stresses while in flight are described (approximately) by mathematical equations. This is the process of “mathematical modeling” in the title of the blog. These equations can’t be solved exactly. For example, there is no way to get a written formula for the air speed at every point around an airplane wing. Thus, the next step is to approximate the solutions to the equations using numerical methods. This field is known as scientific computation and is my original research area. The resulting computational tools can be used to quickly and cheaply test many new airplane designs and optimize performance and safety. So John Kenna came to work at Ballard and with his background expected to have some simulation tools to help with design. However, he discovered that such tools had not yet been developed for the fuel cell industry. He was a guy with vision and thought that these would be a real help to the company. He started by taking a graduate level mathematics course at Simon Fraser University taught by Keith, who was working there at the time. Quite soon, he realized that it would be easier to get Keith involved in the activity than learn the math himself and pushed for the collaborative project with us from within the company.
Keith and I had funding from MITACS, and Ballard and formed a group to develop models and computational simulation tools for hydrogen fuel cells. They are electrochemical systems that combine hydrogen and oxygen (from air) to produce energy. Rather than generating thermal energy through combustion, they generate electrical power with two electrochemical steps (hydrogen separating into protons and then combining with oxygen to form water) separated by a membrane that only conducts protons. This is shown schematically below. In this picture, the red arrows depict hydrogen movement from channels to catalyst sites, green oxygen movement from channels and blue the movement of product water.
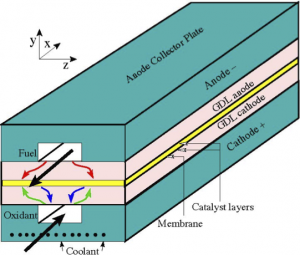
Electrons travel through an external circuit doing useful work. The membrane is a key element to these devices. There are several types of fuel cells. The ones we looked at were low temperature (80 degrees C) devices in which the membrane is a polymer material with acidic side chains. These are Polymer Electrolyte Membrane Fuel Cells (PEMFC). The electrochemical reactions on either side of the membrane have to be catalyzed to run at appreciable rates. Currently, platinum is used as a catalyst. This is one of the limitations to widespread use since platinum is expensive and rare. Some more details of the processes in the Membrane Electrode Assembly (MEA) between the fuel cell channels is shown below.
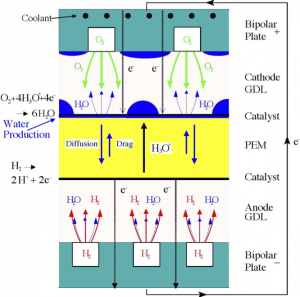
Much of what we did was modeling, that is writing equations that described processes within a fuel cell and then thinking of ways to compute approximations to these models efficiently. These models were what is known as “multi-scale,” since details of processes from channel to channel (about 1mm) affected performance along the length of the cell (up to 1m long) and a number of cells (up to 100) are combined in a fuel cell stack to make appreciable power. Much of what we did is summarized in the review article, PEM Fuel Cell: A Mathematical Overview if you want to see the technical details.
I found some pictures from our group from the early years (late 1990s). Shown below from left to right are me (looking young and using an overhead projector!), Keith Promislow, and Radu Bradean who worked with us as a post-doctoral fellow and then went to a position at Ballard. You can see we had fun with this project.



As mathematicians, we really brought something to this project and this industry. Standard engineering computational tools such as computational fluid dynamics packages are not a good fit to models from this industry due to their multi-scale nature, the stiff electrochemical reaction rates and the capillary dominated two phase flow in the electrodes.
However, I have to say that I was initially reluctant to be involved in the project and viewed it as a distraction from my research work at the time on more abstract questions in scientific computation. In hindsight, I am happy I did get involved, but my initial reservation is common to many mathematicians. In my department (Mathematics at the University of British Columbia) I would say that only 10 of 60 faculty members would be open to an interdisciplinary project like the one I described above and this is a higher ratio than most departments. Concentrating on research in a single, technical, abstract area is seen as the best path to professional success. In some departments (not that uncommon) most of the work I did on this project would not count towards professional advancement (tenure and promotion), since it was not mathematics research but rather the use of “known” mathematics in a new application (known to us but not to the application scientists). I am not advocating that all mathematicians should work on such projects: it was the high-level mathematical training I received in a mathematics-focused environment that gave me the skills to contribute to this project. However, I believe such projects should be encouraged and rewarded. Events like MPE2013 highlight the contributions that mathematicians can make to our world, and I am very happy to be a part of it.
Author Bio: Dr. Brian Wetton was trained at the Courant Institute of NYU. In 1991 he became a faculty member in the Mathematics Department at UBC. He was awarded the Canadian Applied and Industrial Mathematics Society prize for Industrial Mathematics research in 2010 for his work on this project.