One of the most famous images in Japanese art is the Great Wave off Kanagawa, a woodblock print by the Japanese artist Hokusai. The print shows an enormous wave on the point of breaking over boats that are being sculled against the wave’s travel (see Figure 1a). As well as its fame in art, this print is also famous in mathematics: firstly because the structure of the breaking wave at its crest illustrates features of self-similarity, and secondly because the large amplitude of the wave has led it to be interpreted as a rogue wave generated from nonlinear wave effects (see J. H. E. Cartwright, H. Nakamura (2009) Notes Rec. R. Soc. 63, 119–135).
However, we have just published a paper in Notes and Records of the Royal Society (J. M. Dudley, V. Sarano, F. Dias (2013) Notes Rec. R. Soc. 67 doi: 10.1098/rsnr.2012.0066) that points out that whether the generating mechanism is linear or nonlinear does not enter into the definition of a rogue wave; the only criterion is whether the wave is statistically much larger than the other waves in the immediate environment. In fact, by making reference to the Great Wave’s simultaneous transverse and longitudinal localisation, we show that the purely linear mechanism of directional focussing predicts characteristics consistent with those of the Great Wave. We have also been fortunate enough to collaborate with the photographer V. Sarano who has provided us with a truly remarkable photograph of a 6 m rogue wave observed on the Southern Ocean from the French icebreaker Astrolabe, which bears a quite spectacular resemblance to the Hokusai print (see Figure 1b).
Rogue waves can arise from a variety of different mechanisms. For example, linear effects that can generate rogue waves include: spatial focusing due to refraction with varying topography; wave-current interactions; directional focusing of multiple wave trains. Nonlinear effects that have received much attention include the exponential amplification of random surface noise through modulation instability.
In the case of the Great Wave, a clue to how linear effects may play a role is seen by noting the Great Wave’s localization both along its direction of travel and transversally – we see the wave rising from the foreground and ending in the middle ground of the print. This is in fact a characteristic seen in the linear effect of directional focusing, which arises whereby wave trains with different directions and phases interfere together at a particular point. Typical results of numerical modeling of this process are shown in Figure 2. The modeling is based on propagation equations that include both linear and nonlinear effects, but the concentration of energy at the focus arises from linear convergence. Nonlinearity plays a role only as the wave approaches the linear focus where it increases the steepness to the point of breaking.
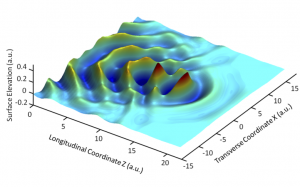
Figure 2 Numerical results showing Directional Focusing of periodic wave trains towards an extreme wave at the focus.
By John M. Dudley, Institut FEMTO-ST, UMR 6174 CNRS-Université de Franche-Comté, Besançon, France and Frédéric Dias, School of Mathematical Sciences, University College Dublin, Ireland.
