A recent blog entry discussed why celestial mechanics is a part of the focus of the MPE2013. Here I suggest a further argument in favor of this inclusion and call attention to some recent events and mathematical ideas in connection with explorations beyond planet Earth.
There is widespread interest in finding and designing spacecraft trajectories to the Moon, Mars, other planets, or other celestial bodies (comets, asteroids), which require as little fuel as possible. This is justified mostly by the cost of the missions: each extra pound of load for a spacecraft roughly costs 1 million dollars. Hence, for robotic space missions, which typically conduct numerous observations and measurements over long periods of time, in order to maximize the equipment load, it is imperative to minimize the fuel consumption of the propulsion system. One way to achieve this is to cleverly exploit, in a mathematically explicit way, the gravitational forces of the Earth, Moon, Sun, etc.
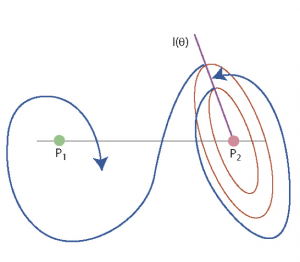
To illustrate the concept, suppose that one would like to design a low-energy transfer from the Earth to the Moon. Of course, first one has to place the spacecraft on some orbit around the Earth, which is unavoidably energy expensive. Surprisingly though, the second leg of the trajectory, to take the spacecraft from near the Earth to some prescribed orbit about the Moon, can be done at a low energy cost (in theory, even for free). Say that we would like to insert the spacecraft at the periapsis of an elliptic orbit about the Moon, of prescribed eccentricity and at some prescribed angle with respect to the Earth-Moon axis. We would like to do that without having to slow down the spacecraft at the arrival (or maybe just a little), thus saving the fuel necessary for such an operation. Imagine that we run the “movie” of the trajectory backwards, from the moment when the spacecraft is on the elliptic orbit. Since the eccentricity is fixed, the semi-major axis determines the velocity of the spacecraft at the periapsis. If the semi-major axis is too short (or, equivalently, the velocity is too low) the trajectory will turn around the Moon without leaving the Moon region; such a trajectory is redeemed as ‘stable’. By gradually increasing the semi-major axis (hence, the velocity), one will find a trajectory that leaves the Moon region and makes a transfer to the Earth region; such a trajectory is redeemed as ‘unstable’. See Fig. 1.
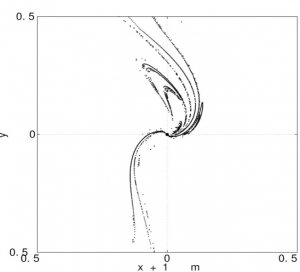
The critical values of the semi-major axis which delineates the stable motions from the unstable ones are called “weak stability boundary” points. Exploring all angles of insertion and all values of the eccentricity of the elliptical orbit yields a “weak stability boundary” set; this appears to be some sort of a fractal. See Fig. 2.
All points in the weak stability boundary correspond to arrival points of low energy transfers from the Earth to the Moon. The spacecraft trajectories designed by this method yield fuel savings of 10-15%.
The notion of a weak stability boundary was introduced by Edward Belbruno (Princeton University) in 1987; a documentary trailer on the discovery of this concept can be found on YouTube. The method was successfully applied, for the first time, for the rescue of the Japanese lunar mission Hiten in 1991. The recent mission GRAIL (Gravity Recovery and Interior Laboratory) of NASA, which took place in 2012, used the same transfer as Hiten. The purpose of this mission was to obtain a high-resolution mapping of the gravitational field of the Moon. For this purpose, two spacecrafts were placed on the same orbit about the Moon, and their instruments measured the changes in the relative velocity very precisely; such changes were translated into changes of the gravitational field. (This technique had been tested previously for the mapping of Earth’s gravity, as a part of the mission GRACE – Gravity Recovery and Climate Experiment – a joint mission of NASA and the German Aerospace Center, since 2002.) A key point for the GRAIL mission was to place the two spacecrafts on precisely the same lunar orbit; the weak stability boundary concept was quite suitable for this purpose.
A deeper understanding of the weak stability boundary can be achieved from studying hyperbolic invariant manifolds. The motion of a spacecraft relative to the Earth-Moon system can be modeled through the three-body problem. In this model, the intertwining gravitational fields of the Earth and the Moon determine some “invisible pathways,” called stable and unstable manifolds, on which optimal transport is possible. These manifolds have been found in the works of Henri Poincaré. It turns out, surprisingly, that these manifolds are deeply related to the weak stability boundary. More precisely, under some energy restriction, it can be geometrically proved that the weak stability boundary points lie on certain stable manifolds.
Here are some recent references:
Belbruno, E.; Gidea, M; Topputo, F. Weak stability boundary and invariant manifolds. SIAM J. Appl. Dyn. Syst. 9 (2010), no. 3, 1061–1089.
Belbruno, E.; Gidea, M.; Topputo, F. Geometry of Weak Stability Boundaries. Qual. Theory Dyn. Syst. 12 (2013), no. 1, 53–66.
Marian Gidea
School of Mathematics
Institute for Advanced Study
Princeton
and
Department of Mathematics
Northeastern Illinois University
Chicago